|
The smallest values of momentum, angular momentum and energy in the Universe
By Louis Nielsen Introduction In the following I shall perform a general rational quantization of some of the physical quantities and equations we meet in classical mechanics. This general quantization is a direct consequence of the quantization of space, time and mass. The existence of this basical quantization - and the cosmological consequences hereof - I have accounted for in my holistic quantum cosmology. The basis for the following - and my holistic quantum cosmology - is the existence of the following fundamental cosmological quantities:
These cosmological quantities define an absolute and
cosmological system of units, independent of specific
local systems and the existence of living systems.
(See chapter 5 in my treatise).
As a consequence of the quantization of the physical quantities, all laws and formular connections in our description of the Universe will be quantized, viz. in the equations will appear characteristic rational quantum numbers. As a consequence hereof it will be possible to formulate the laws of nature as quantum number conditions. The expression holistic refers to the fact, that in the physical expressions appear quantities as well from microcosmos, f.i. Planck's constant and the mass of an uniton, as also from macrocosmos, f.i. the total mass of the Universe. As a consequence of the basical quantization of the fundamental physical
quantities, all natural phenomena must - fundamentally seen - be
described by a discrete mathematics and not, as it has been usual
since Newton, by a continuous mathematics. As elementary length, and the
corresponding elementary time, are extremely small quantities - when
given by our practical measuring units - daily and macroscopic phenomena
can still, adventageously and with great accuracy, be described by
means of continuous mathematics. If you, on the contrary, wish a
correct description and understanding of micro physical phenomena
and the earliest states in the evolution of the Universe, then it is
necessary to use a discontinuous mathematics. In an earlier chapter I have
considered some consequences of what I call a physical quantum geometry.
With the existence of a physically smallest ’distance standard’, we can not
give a sophisticated description of nature by means of the continuous
Euclidic geometry. In a physical quantum geometry, we must quantize the
geometrical distance dimensions of f.i. a ’circle’ so that the quotient
between the 'quantum perimeter' and the 'quantum diameter' of the quantum
circle defines a rational pi, I shall show that the maximal work, which was carried out in the Universe, when it was 'born' within the first cosmic quantum time interval, is given by the total mass of the Universe multiplied by the square of the velocity of light. The magnitude of this maximal work is equal to the total energy, which broke out in the Universe, when it performed its first cosmic quantum jump over elementary length! Using my quantum cosmological equation, connecting the total mass of the Universe with the mass of a uniton, I can in a simple way derive the famous equation E = m · c02 , where m is the mass of a system and c0 is the velocity of light. In the following I shall consider the quantum conditions of some special systems, a.o. the quantized motion of a particle, moving in a homogenous gravitational field. I shall show that the energy of a particle or a given system can either be given as a rational fraction of the total energy of the Universe, or as a whole multiple of the kinetic energy of a uniton.
Quantization of space, time and mass. Quantum kinematics and quantum dynamics The physically smallest distance in the Universe - elementary length, r0, and the physically smallest time interval - elementary time, t0, are given by: (1) 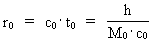 where h is Planck's constant, M0 the total energy/matter mass of the Universe and c0 the light constant. Any finite physical distance (2) 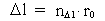 where Any finite physical time interval (3) 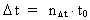 where As a natural consequence of (2) and (3) also the physical quantities velocity and acceleration will be quantized. For a particle, moving in a given reference system, we define the quantized velocity v - in a given direction - as the travelled distance divided by the elapsed time interval. Using the basically quantized quantities in (2) and (3) we get for v: (4) 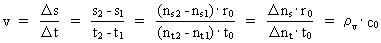 where (5) 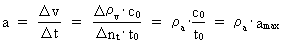 where It must be assumed that the mass m of any system is a rational fraction of the total mass of the Universe M0, viz.: (6) 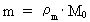 where In a given reference system we shall define the quantized momentum p of a particle - in a given direction - by the following: (7) 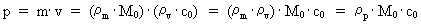 where
Quantum force and quantum work If a particle in a given reference system accelerates, viz. changes velocity, we say that the particle is influenced by one or more forces. The magnitude Fres of the total influence of forces on the particle, also called the resulting force, we define as the change in the momentum of the particle divided by the corresponding time interval, viz.: (8) 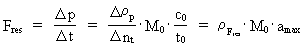 In equation (8) The work, AF, done by a constant force over a distance
(9) 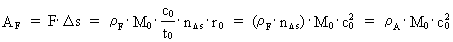
The quantity M0· c02 is - as I shall show in the following - the total energy in the Universe! The content of energy in any subsystem is thus equal to a rational fraction of the total energy of the Universe! A work done on a system means that there has been an exchange of
energy between the systems exchanging forces. The magnitude of the work,
Ares, done by the resulting force on a
particle, is equal to the increase of the kinetic energy of the particle,
(10) 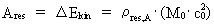
The embryonic work of the Universe and its total content of energy When the Universe was 'born' and performed its first cosmical quantum jump over a distance equal to elementary length, the total energy, existing in the Universe, came into being. This total energy has since then been distributed as kinetic energy of all the smallest matter/energy quanta - the unitons - of which everything in the Universe consist. We can calculate this total cosmic energy, Ekin,cos, by calculating the maximum physical work Amax, which was done over elementary length r0: (11) 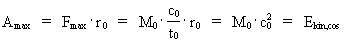 We see that the total energy of the Universe is equal to the product of its total mass and the velocity of light squared, thus an expression corresponding to what Einstein found in his special theory of relativity from 1905. Here, however, I arrived to the expression by a quantum physical method, and thereby in a fundamentally different way!
Derivation of the formula E = m·c02 and a uniton-mechanical explanation In my holistic quantum cosmology (see this) I show the existence of the following connection: (12) 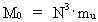 where N3 is the cosmic evolution quantum number, which controls the evolution of the Universe and is a discrete parameter, ’ticking’ up through the natural numbers. N is equal to the actual quotient between the electrostatic and the gravitostatic forces between two electrons. mu is the mass of a uniton. From (12) we see that in any state of the Universe N3 unitons exist. In our epoch N3 = 7,2 · 10127, meaning an extremely high number of unitons. Any limited amount of matter consists of a definite number of unitons. Inserting the expression from (12) in equation (11) we get: (13) 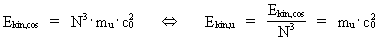 From equation (13) we see that the kinetic energy of one uniton
Ekin,u is determined by the product of the mass of a uniton
and the velocity of light squared! This uniton-kinetic energy is the
physically smallest amount of energy - elementary energy - in the
actual Universe. (14) 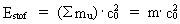 The total content of energy Emat of a definite
amount of matter is thus given by the product of its mass
and the velocity of light squared!
The smallest values of momentum, angular momentum and energy of our Universe Using the connection given by equation (12) we can express the content of energy of different systems as a whole multiplum of the kinetic energy of one uniton. As a particle we shall understand a limited uniton- dynamical system, consisting of a definite number of unitons. The uniton defined mass m of the particle is given by: (15) 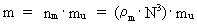 where nm is a natural number, the mass quantum number.
(16) 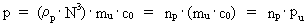 where np is a natural number, the natural momentum
quantum number. (17) 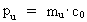 gives the smallest physical momentum - elementary momentum - in the Universe. If this elementary momentum is multiplied by the extension R of the Universe, we get the physical quantity called angular momentum. The product of pu and R gives Planck's constant h, viz. the following is valid: (18) 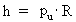 It will be seen that Planck's constant is not as fundamental as presumed in established physics. Elementary momentum and the extension of the Universe must be considered more fundamental! The expression in equation (18) is a limit case of Heisenberg's uncertainty relations regarding momentum and position, as it gives the context between minimum uncertainty for momentum and maximum uncertainty for position. Multiplying the elementary momentum by elementary length, r0, we can find the value of the physically smallest angular momentum in the Universe, elementary angular momentum lu: (19) 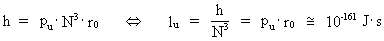 We see that the value of elementary angular momentum is extremely small
given by SI-units, as defined by men. If we, on the contrary, give
elementary angular momentum in cosmological units, then the
value is equal to 1 (masson · spaton²)/tempon. (20) 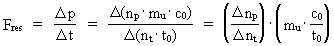 where Equations (10) and (11) can be transformed to: (21) 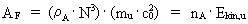 (22) 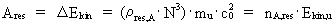 where nA and nA,res can be considered as natural
work quantum numbers. Ekin,u is the kinetic
energy of one uniton, and this is the physically smallest amount
of energy in the Universe - elementary energy. In cosmological units
the value of elementary energy is equal to 1.
(23) 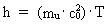 viz. as a product of elementary energy and the age of the Universe. Equation (23) is, like equation (18), a limit case of Heisenberg's uncertainty relations for time and energy. The quantum motion of a particle in a homogenous gravitational field Let us analyse the state of energy of a particle, moving in a homogenous gravitational field, using the quantized expressions of energy. The kinetic energy Ekin of a particle can be written: (24) 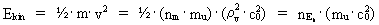 where m is the mass of the particle, equal to a natural number multiplied
by the mass of a uniton. v is the rationally quantized velocity, and
nEk is a natural number - the kinetic energy quantum
number. From (24) we see that the kinetic energy of the particle
is given by a whole multiple of the elementary energy.
(25) 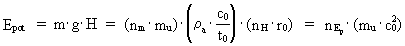 where g is the acceleration of gravity at the position, equal to a rational acceleration quantum number multiplied by the universal maximum acceleration - the quotient between the velocity of light and elementary time. H is the vertical height measured from a chosen origo and determined by a space quantum number multiplied by the elementary length. nEp is the energy quantum number, corresponding to the potential energy - the potential energy quantum number. We see from (25), that also the gravitational potential energy can be calculated as a whole multiple of the elementary energy. A particle, moving in the homogenous gravitational field, has within each quantum time interval a total socalled mechanical energy, Emek, given by: (26) 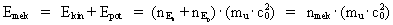 where nmek is the mechanical energy quantum number.
(27)  During the motion of the particle we thus have: (28) 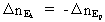 Expressed in words equation (28) means: The kinetic energy quantum number will increase just as must as the potential energy quantum number decreases! If for instance the potential energy quantum number decreases by 10, it means that the kinetic energy quantum number will increase by 10. In practical life the change of these numbers will be extremely great. But fundamentally seen, it must be assumed that nature functions as I have described!
© Louis Nielsen, July 1998
|
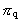 Likewise the pythagoreic relations will not be valid in a physical quantum
geometry.
Likewise the pythagoreic relations will not be valid in a physical quantum
geometry.
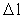 is given by:
is given by:
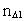 is a natural number,
the space quantum number.
is a natural number,
the space quantum number.
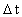 is given by:
is given by:
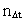 is a natural number, the time quantum number.
is a natural number, the time quantum number.
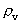 is a rational velocity quantum number, which can take rational
values between 0 and 1.
is a rational velocity quantum number, which can take rational
values between 0 and 1.
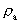 is a rational acceleration quantum number, which can take
rational values between 0 and 1. amax is equal to
the quotient between the velocity of light and elementary time and is thus
a maximal greatest physical acceleration in the Universe. The maximum
acceleration occurred when the Universe, with its matter and motions, was
'born' within the first cosmic quantum jump over a distance equal to
elementary length!
is a rational acceleration quantum number, which can take
rational values between 0 and 1. amax is equal to
the quotient between the velocity of light and elementary time and is thus
a maximal greatest physical acceleration in the Universe. The maximum
acceleration occurred when the Universe, with its matter and motions, was
'born' within the first cosmic quantum jump over a distance equal to
elementary length!
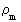 can be called the cosmic mass quantum number.
can be called the cosmic mass quantum number.
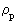 is the rational momentum quantum number, which can take rational
value between 0 and 1.
is the rational momentum quantum number, which can take rational
value between 0 and 1.
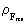 is a rational force quantum number, which can take rational
values between 0 og 1.
is a rational force quantum number, which can take rational
values between 0 og 1.
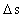 can - if the directions of force and motion are parallel- be defined as:
can - if the directions of force and motion are parallel- be defined as:
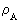 defines a rational
work quantum number, or energy quantum number, which can
take rational values between 0 og 1.
defines a rational
work quantum number, or energy quantum number, which can
take rational values between 0 og 1.
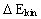 From (9) we get for the work done by the resulting force:
From (9) we get for the work done by the resulting force:
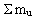 of the masses of the unitons of which the amount of matter consists,
the following is valid:
of the masses of the unitons of which the amount of matter consists,
the following is valid:
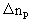 and
and 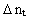 give the corresponding increases in momentum quantum number and time quantum
number, respectively.
give the corresponding increases in momentum quantum number and time quantum
number, respectively.