|
The Extension, Age and Mass of the Universe, calculated by means of atomic physical quantities and Newton's gravitational 'constant' By Louis Nielsen, Senior Physics Master, Herlufsholm, Denmark Introduction. In the following I shall show that there is an intimate - holistic - context between microcosmos - the atomic world - and macrocosmos - the Universe as a whole. I shall deduct equations allowing us to calculate cosmological quantities as the age, extension and total mass of the Universe by means of atomic physical quantities and Newton's gravitational 'constant'. The only quantity, which has not yet been measured with great accuracy, is the extension of the electron, but it is supposed to be of the order smaller than 10—18 m. The deducted equations are based on my discovery of two equations — # (1) and (2) — establishing connections between physical quantities from microcosmos, f.i. Planck's Constant, the mass of an electron, its extension and electrical charge, and quantities characteristical for the Universe as a whole, such as its mass, extension and age, and furthermore the velocity of light and Newton's gravitational constant. The discovered equations form part of my quantum cosmology, with the main title: 'Holistic Quantum Cosmology with Decreasing Gravity'. The treatise is found on the Internet at the URL: http://louis.rostra.dk/.
The cosmologic basic equation
As my equation, given by (1), gives a context between quantities characterizing microcosmos and quantities characterizing macrocosmos I call it for the cosmologic basic equation: (1) 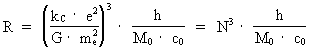
In equation (1) R is the actual extension of the Universe,
kC
is Coulomb's Constant, e is the electric charge of
the electron, meits mass,
G Newton's gravitational 'constant',
h Planck's Constant, c0 is the velocity of light and
M0 is the total matter/energy of the Universe.
The fraction in the first parenthesis, denominated N = 4.16 ·
1042, gives the ratio between the electrostatic forces
and the gravitostatic forces between two electrons. The ratio
between Planck's Constant and the product of the total mass of the
Universe and the velocity of light gives the physical smallest
distance in the Universe and is therefore called the elementary
length.
The ratio between the mass density of the electron and the mass density of the Universe.
Let us calculate the ratio between the mass density,
(2) 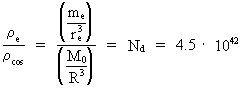
In (2) the following values are used: R = 1026 m ;
re =0.5·10—18 m ; me
= 9.11·10—31 kg;
M0 = 1.6·1060 kg.
Calculation of the extension, age and mass of the Universe. Combining (1) and (2) we can calculate the extension, R, of the Universe by the following equation: (3) 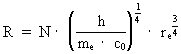 If we for the extension of the electron, re use the value 0.5·10—18 m we get for for R: (4) 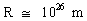 which of course is not surprising. R can also be written as: (5) 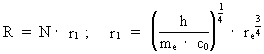
where r1 gives a characteristic length:
r1 = 2.4 · 10–17 m
(6) 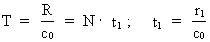
where t1 gives a characteristic time interval:
t1 = 7.8 · 10–26 s.
(7) 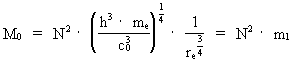
where m1 is a characteristic mass:
m1 = 9.2 · 10–26 kg.
Decreasing gravity and the increasing electron. From the deducted equations it can be seen that with an expanding Universe, where R is increasing, one or more of the used quantities must vary, gradually as the Universe expands. The question is: Which of the quantities varies? There are many indications that G decreases as the Universe expands. This is treated in my quantum cosmology, where it is also assumed that the mass of the Universe is kept constant. As it is also assumed that the mass of the electron is constant, this leads to the observation that the extension of the electron must vary, gradually as the Universe expands. The calculations show (see above reference) that the extension of the electron increases. In other words: The electron is growing! For the temporal relative increase of the extension of the electron the following is valid: (8) 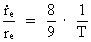 where T is the actual age of the Universe. We see from equation (8) that the increase of the electron is extremely small in our epoch, about 8.5·10–11 per year. In earlier epochs of the Universe the increase has been faster. In other words, the electron has been smaller when the Universe was younger. This also seems to be a logical evolution, for how could there otherwise be space enough for electrons in the very earliest and extremely much smaller Universe? If you ask: does the extension of protons and other composite particles also vary as the Universe expands? Then the reply must be Yes!
©
Louis Nielsen, 20. nov. 1997
|