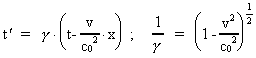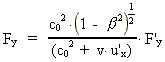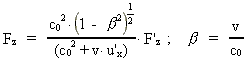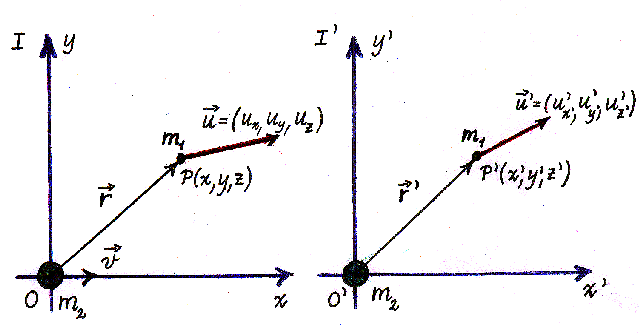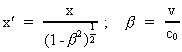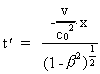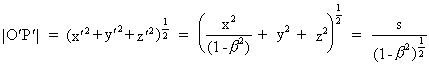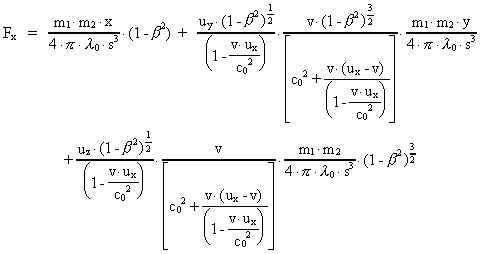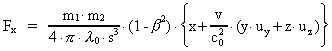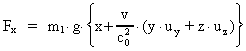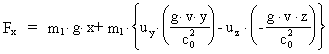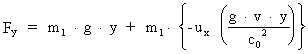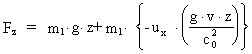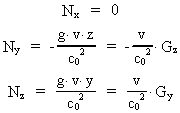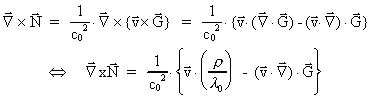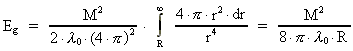|
En Maxwell-analog gravitationsteori
med to gravitationsfelter
af Louis Nielsen
Indledning
Jeg vil i denne artikel vise, at det gravitationelle rotationsfelt, som jeg
indførte i en tidligere artikel (Louis Nielsen,
 nr. 9 (1972)),
er en konsekvens af den specielle relativitetsteori. nr. 9 (1972)),
er en konsekvens af den specielle relativitetsteori.
De beregninger, som her gennemføres, benyttes, når man vil vise,
at det magnetiske induktionsfelt er en relativistisk korrektion til
elektrostatikken. Man kan nemlig vise, at Maxwells ligninger er en
konsekvens af:
- Coulombs elektrostatiske kraftlov
- den specielle relativitetsteori
- elektrisk ladnings invarians
Det er ligeledes vist, at oprindelsen til det magnetiske induktionsfelt er
at finde i den relativistiske Thomas-rotation. En analog argumentation
fører til eksistensen af et gravitationelt rotationsfelt.
Udledning af de gravitationelle feltligninger
Jeg vil nu udlede de feltligninger, som det gravitostatiske felt
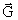 og det gravitationelle rotationsfelt og det gravitationelle rotationsfelt
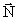 skal opfylde. Jeg benytter følgende
udgangspunkter og antagelser: skal opfylde. Jeg benytter følgende
udgangspunkter og antagelser:
a) Newtons gravitostatiske kraftlov
b) Den specielle relativitetsteoris transformationsligninger for
steder, tider, hastigheder og kræfter
c) Antagelsen, at den gravitationelle masse er Lorentzinvariant
Ad a):
Newtons kraftlov for hvilende gravitationelle ladninger (lig gravitationelle
masser) vil jeg skrive på formen:
(1) 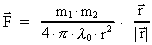
hvor m1 og m2 er de gravitationelle masser
af to partikler, r afstanden mellem dem, og
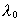 en negativ
parameter, som hænger sammen med Newtons gravitationskonstant G
efter formlen: en negativ
parameter, som hænger sammen med Newtons gravitationskonstant G
efter formlen:
(2) 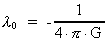
Vi vil overalt benytte SI-enhedssystemet. Da vi ikke sætter noget
minustegn i (1), må 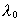 nødvendigvis være negativ for de gravitationelle
masser, som vi kender til i vor del af universet, da vi jo altid erfarer,
at gravitationelle masser med samme fortegn tiltrækker hinanden. nødvendigvis være negativ for de gravitationelle
masser, som vi kender til i vor del af universet, da vi jo altid erfarer,
at gravitationelle masser med samme fortegn tiltrækker hinanden.
Vi ser, at ligning (1) er matematisk identisk med Coulombs kraftlov
for hvilende elektriske ladninger:
(3) 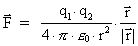
hvor nu q1 og q2 er de elektriske ladninger og
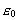 vacuums
dielektricitetskonstant. Fysikken bag ligningerne (1) og (3) er
ikke identisk. Dette svarer f.eks. til, at fysikken bag
vandbølger og elektromagnetiske bølger ikke er identisk, men
den matematiske beskrivelse er identisk. Et andet eksempel,
blandt talrige, afspejles i fænomenerne spin og isospin, hvor
den matematiske struktur igen er identisk, hvorimod fysikken er forskellig.
Denne matematiske isomorfi (samme form) er en erkendelse, man bør
holde sig for øje. vacuums
dielektricitetskonstant. Fysikken bag ligningerne (1) og (3) er
ikke identisk. Dette svarer f.eks. til, at fysikken bag
vandbølger og elektromagnetiske bølger ikke er identisk, men
den matematiske beskrivelse er identisk. Et andet eksempel,
blandt talrige, afspejles i fænomenerne spin og isospin, hvor
den matematiske struktur igen er identisk, hvorimod fysikken er forskellig.
Denne matematiske isomorfi (samme form) er en erkendelse, man bør
holde sig for øje.
Ad b):
Vi vil antage, at vi kan benytte transformationsformlerne fra den
specielle relativitetsteori. Vi vil benytte Lorentz-transformationen:
(4) 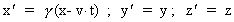
(5) 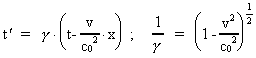
og transformationsformlerne for kraftkomponenterne:
(6) 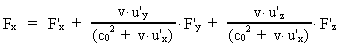
(7) 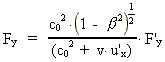
(8) 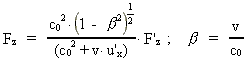
De umærkede størrelser er bestemt i forhold til
inertialsystemet I, de mærkede i forhold til inertialsystemet I', der
bevæger sig med hastigheden v ud ad x-aksen i I. u' er en partikels
hastighed i I'. Størrelsen c0 er en naturkonstant, der
svarer til en fotons hastighed i feltfrit vacuum. Ved begrebet
feltfrit vacuum vil jeg forstå et område af rummet, der er
absolut frit for både felter og stof.
Ud over ligningerne (4) til (8) vil vi benytte transformationsformlerne
for hastigheder.
Ad c):
Antagelsen, at den gravitationelle masse er Lorentz-invariant, kan kun tages
som en approximation, idet det strider imod ækvivalensprincippet.
Ækvivalensprincippet kan formuleres som princippet om identiteten
mellem den inertielle og den gravitationelle masse.
Da den inertielle masse vokser med hastigheden, må, ifølge
ækvivalensprincippet, også den gravitationelle masse vokse
på samme måde. Dette forekommer intuitivt meget mærkværdigt.
Vi betragter nu to inertialsystemer I og I':
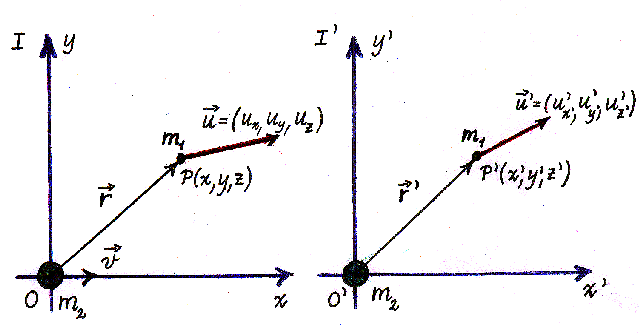 I inertialsystemet I bevæger den gravitationelle masse m2
sig med hastigheden v. Inertialsystemet I' bevæger sig med hastigheden
v i forhold til I og ud ad dette systems x-akse. Massen m2 er
da i hvile i I', og vi antager, at den er beliggende i O', begyndelsespunktet
for I'. Vi vil beregne kraften på en partikel med massen m1,
der til tiden t=0 er i punktet P målt i forhold til systemet I.
Partiklen m2 er da netop i punktet O i I. Til tiden t=0 har massen
m1 hastigheden
I inertialsystemet I bevæger den gravitationelle masse m2
sig med hastigheden v. Inertialsystemet I' bevæger sig med hastigheden
v i forhold til I og ud ad dette systems x-akse. Massen m2 er
da i hvile i I', og vi antager, at den er beliggende i O', begyndelsespunktet
for I'. Vi vil beregne kraften på en partikel med massen m1,
der til tiden t=0 er i punktet P målt i forhold til systemet I.
Partiklen m2 er da netop i punktet O i I. Til tiden t=0 har massen
m1 hastigheden
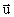 = (ux,
uy, uz) i I og tilsvarende = (ux,
uy, uz) i I og tilsvarende
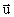 ' = (u'x,
u'y, u'z) i I'. I inertialsystemet I' har man til tiden
t=0 i I: ' = (u'x,
u'y, u'z) i I'. I inertialsystemet I' har man til tiden
t=0 i I:
(9) 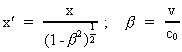
(10) 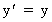
(11) 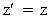
(12) 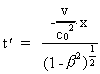
Heraf får vi for afstanden |O'P'|:
(13) 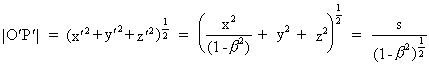
hvor s er defineret ved: s = (x² + (1-ß²) ·
(y² + z²))1/2
Den numeriske værdi af kraften F' på massen m1 i
punktet P' vil til tiden t' = - v/c0²·x·(1-ß²)-1/2,
altså til tiden t=0 i I, være givet ved:
(14) 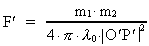
eller i komponenter langs x'-, y'-, z'-akserne:
(15) 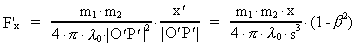
(16) 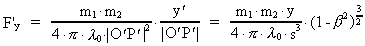
(17) 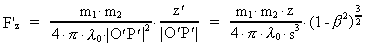
Ved indsættelse af (15) i transformationsligningen (6) får man:
(18) 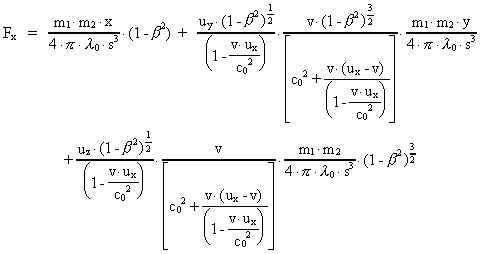
Dette kan omskrives til:
(19) 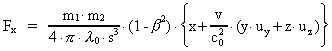
eller:
(20) 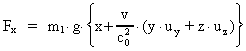
hvor g er defineret ved:
(21) 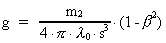
For de andre komponenter får man ved hjælp af
transformationsligningerne:
(22) 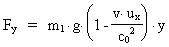
(23) 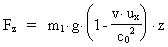
Ligningerne (20), (22) og (23) angiver kraftkomponenterne målt i
forhold til inertialsystemet I. Vi ser, at kraften mellem partiklerne
afhænger af disses hastigheder i forhold til systemet I.
Ligningerne (20), (22) og (23) sætter os nu i stand til at
definere et nyt gravitationsfelt på en sådan måde, at
disse kan sammenfattes i en gravitationel kraftlov af formen:
(24) 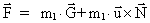
eller udskrevet i komponenter:
(25) 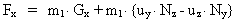
(26) 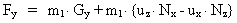
(27) 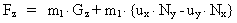
Idet vi omskriver ligning (20) til formen:
(28) 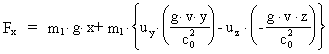
og sammenligner med (25), konkluderer vi, at
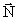 -feltet er defineret ved: -feltet er defineret ved:
(29) 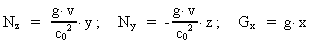
Tilsvarende får vi ved sammenligning mellem ligningen:
(30) 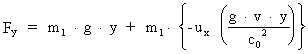
med (26), at:
(31) 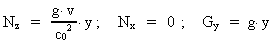
Endelig giver sammenligning mellem:
(32) 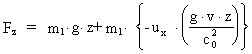
og (27), at:
(33) 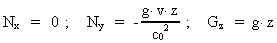
Vi har således vist, at i inertialsystemet I er
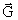 -feltet bestemt ved: -feltet bestemt ved:
(34) 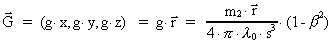
hvor 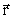 er stedvektoren til punktet P.
Vi ser, at er stedvektoren til punktet P.
Vi ser, at 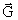 -feltet afhænger af
farten v, hvormed massen m2 bevæger sig i forhold til
systemet I. -feltet afhænger af
farten v, hvormed massen m2 bevæger sig i forhold til
systemet I.
Samler vi komponenterne for
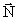 -feltet: -feltet:
(35) 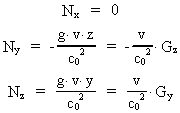
ser vi, at det har natur af et rotationsfelt. Ligningerne i (35) er
ensbetydende med følgende vektorligning:
(36) 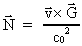
Vi kan nu opstille en rotationsligning for
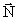 -feltet
ved at operere med rotationsoperatoren -feltet
ved at operere med rotationsoperatoren
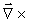 på begge sider af lighedstegnet i ligning (36).
på begge sider af lighedstegnet i ligning (36).
Vi får:
(37) 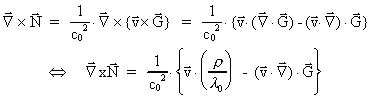
Det sidste led i (37) kan vi omskrive som følger:
Da 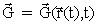 følger
heraf, at den totale
afledede af følger
heraf, at den totale
afledede af
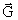 er givet ved: er givet ved:
(38) 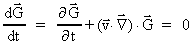
den totale afledede angiver
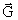 's
ændring pr. tidsenhed, når man følger med feltet, som
da er konstant. Den totale afledede er således nul, og vi har: 's
ændring pr. tidsenhed, når man følger med feltet, som
da er konstant. Den totale afledede er således nul, og vi har:
(39) 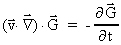
som indsat i (37) giver:
(40) 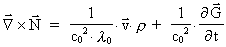
Ved indførelse af »vacuums gravitationelle permeabilitet«
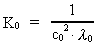 og
massestrømtæthedsvektoren og
massestrømtæthedsvektoren
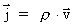 har vi sluttelig
ligningen: har vi sluttelig
ligningen:
(41) 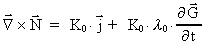
I ligning (37) har vi benyttet, at:
(42) 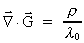
hvilket er en ækvivalent, men dog mere generel ligning end Newtons
gravitostatiske kraftlov (1). Ligning (42) kan vi anskueliggøre
således: Lad massen m2 befinde sig i centrum af en
kugleflade med radius r. På overfladen er
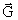 -feltet
radiært og givet ved: -feltet
radiært og givet ved:
(43) 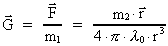
Integration over fladen og benyttelse af Gauß's integralteorem giver:
(44) 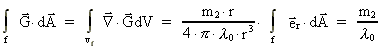
Ved grænseovergangen til et lille volumen omkring m2 får
man (42), idet:
(45) 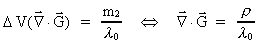
Vi mangler nu ligningerne for 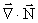 og og 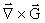 . .
Som en antagelse, men absolut ikke som givet, vil vi betragte
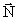 -feltet som kildefrit, dvs. som et rent
hvirvelfelt. Vi antager således, at divergensen af -feltet som kildefrit, dvs. som et rent
hvirvelfelt. Vi antager således, at divergensen af
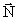 -feltet er forsvindende, udtrykt: -feltet er forsvindende, udtrykt:
(46) 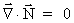
Det kan naturligvis godt tænkes, at der eksisterer N-felt-monopoler,
og (46) må da modificeres til:
(47) 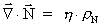
hvor 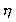 er en konstant,
og er en konstant,
og 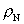 er tætheden
af er tætheden
af 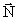 -felt-monopoler. -felt-monopoler.
Vi skal nu bestemme en ligning for 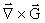 . Vi kunne nu gå tilbage til de oprindelige
transformationsligninger og så bestemme . Vi kunne nu gå tilbage til de oprindelige
transformationsligninger og så bestemme
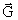 udtrykt ved udtrykt ved
 og og
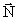 . Dette vil vi dog
ikke gøre,
men blot angive resultatet: . Dette vil vi dog
ikke gøre,
men blot angive resultatet:
(48) 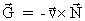
Et argument for ligning (48) kunne måske formuleres ved hjælp af
kraftloven (24).
Lad der være givet et
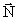 -felt, og lad
os betragte et bestemt punkt i dette. Lad en partikel ankomme til punktet
og heri have hastigheden -felt, og lad
os betragte et bestemt punkt i dette. Lad en partikel ankomme til punktet
og heri have hastigheden
 . Vi ønsker,
at partiklen skal forlade punktet med uforandret hastighed . Vi ønsker,
at partiklen skal forlade punktet med uforandret hastighed
 . Dette kræver, at . Dette kræver, at
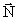 -feltet i punktet skal ændre sig
på en sådan måde i tiden, at kraften på partiklen
er nul. Hvis vi antager, at en ændring af -feltet i punktet skal ændre sig
på en sådan måde i tiden, at kraften på partiklen
er nul. Hvis vi antager, at en ændring af
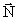 -feltet i tiden inducerer et -feltet i tiden inducerer et
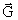 -felt, ser vi af (24), at: -felt, ser vi af (24), at:
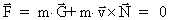 , hvilket giver
(48). Ved operation med rotationsoperatoren , hvilket giver
(48). Ved operation med rotationsoperatoren
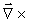 får vi af (48): får vi af (48):
(49) 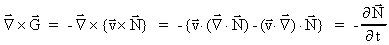
da 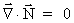 og og
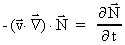 . .
Jeg har hermed vist, at den specielle relativitetsteori kræver
eksistensen af to gravitationelle vektorfelter, karakteriseret
ved 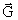 -feltet og -feltet og
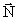 -feltet. -feltet.
Jeg har således demonstreret, at der må gælde
følgende gravitationelle feltligninger (hvis vi ser bort fra
N-felt-monopoler):
(50) 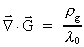
(51) 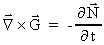
(52) 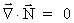
(53) 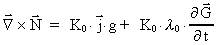
samt kraftloven, som definerer
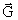 - og - og
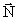 -felterne: -felterne:
(54) 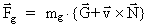
Disse ligninger er i deres primærstruktur matematisk identiske med
Maxwells elektrodynamiske feltligninger for det elektriske
 -felt og det magnetiske induktionsfelt -felt og det magnetiske induktionsfelt
 , idet disse felter adlyder ligningerne: , idet disse felter adlyder ligningerne:
(55) 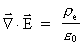
(56) 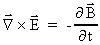
(57) 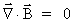
(58) 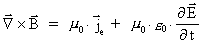
samt kraftloven, som definerer
 - og - og
 -felterne: -felterne:
(59) 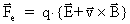
Her er
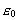 vacuums dielektricitetskonstant
og vacuums dielektricitetskonstant
og 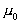 vacuums magnetiske permeabilitet. vacuums magnetiske permeabilitet.
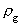 er den gravitationelle massetæthed
og er den gravitationelle massetæthed
og 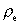 den
elektriske ladningstæthed. den
elektriske ladningstæthed.
Krydshenvisninger:
- En to-vektorfelt gravitationsteori med
variable koblings-»konstanter«
- Centrifugal- og corioliskraftens identitet
med N¯-felt-kraften
Ulineære feltligninger. Indførelse af negative
gravitationelle masser
Trods den primære matematiske lighed mellem de to teorier, som er
udtrykt ved de to ligningssæt (50) til (54) og (55) til (59), så
er den fysiske forskel dog stor. Det forholder sig nemlig således, at
den Maxwellske elektrodynamiske teori er lineær, hvorimod den
her opstillede gravitationsteori er ulineær. Denne ulinearitet
er en konsekvens af Einsteins masse-energi-relation sammenholdt med
ækvivalensprincippet. Einsteins masse-energi-relation udsiger, at en
hvilken som helst energi E har en inerti svarende til en inertiel
masse mi givet ved:
(60) 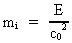
Dette er et resultat af den specielle relativitetsteori og er således
kun et udsagn om den inertielle masse. Ækvivalensprincippet, som er
grundlaget for Einsteins generelle relativitetsteori, kan formuleres:
Hvis en partikel har en inertiel masse mi, da vil der til denne
partikel også være knyttet en gravitationel masse mg
af samme størrelse som mi, dvs. at der gælder:
(61) 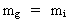
Dette resultat betyder, at der til enhver energi E også er knyttet en
ækvivalent gravitationel masse mg givet ved:
(62) 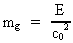
Da der i gravitationsfeltet er en energitæthed, svarer dette til en
ækvivalent massetæthed givet ved (62). Denne massetæthed
er kilde for et nyt gravitationsfelt osv.
Denne specielle vekselvirkning mellem felt og masse bevirker, at de
gravitationelle feltligninger bliver ulineære. Vi vil undersøge
dette forhold lidt nærmere. Først vil vi, for simpelheds skyld,
betragte en hvilende gravitationel masse mg. Denne masse skaber
et gravitostatisk felt
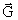 bestemt ved
ligningen: bestemt ved
ligningen:
(63) 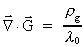
Det kan vises, at feltet (i lighed med feltet omkring en hvilende
elektrisk ladning) indeholder en energitæthed Ug givet
ved:
(64) 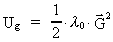
Da 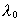 er negativ,
ser vi, at energitætheden i feltet er negativ. Ifølge
(62) svarer dette til en negativ gravitationel massetæthed. er negativ,
ser vi, at energitætheden i feltet er negativ. Ifølge
(62) svarer dette til en negativ gravitationel massetæthed.
(65) 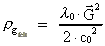
Hvis (62) er eksakt og generelt gyldig, må vi heraf konkludere:
Der eksisterer negative gravitationelle masser. Dette resultat er yderst
interessant, samtidig med at det tilfredsstiller vor symmetriske sans.
Om fortolkningen er sand, kan dog diskuteres. Ækvivalensprincippet
udtrykt i ligning (61) bevirker, at en negativ gravitationel masse må
tillægges en negativ inertiel masse, hvilket forekommer ret
så bemærkelsesværdigt. Hvis (61) er generelt gyldig, må
negative inertielle masser blive konsekvensen af negative gravitationelle
masser.
Massetætheden (65) giver anledning til et
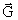 -felt, som kobler
med det oprindelige, således, at det totale -felt, som kobler
med det oprindelige, således, at det totale
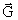 -felt må
bestemmes af ligningen: -felt må
bestemmes af ligningen:
(66) 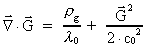
Ligning (66) er en ulineær differentialligning, hvilket bevirker, at
den er ret så kompliceret at løse. Hvis gravitationsfelterne
er relativt svage, kan man linearisere ligningerne. F.eks. vil sidste led
i (66) 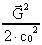 være forsvindende i
forhold til være forsvindende i
forhold til
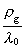 , hvis vi f.eks.
betragter jordkloden. , hvis vi f.eks.
betragter jordkloden. 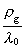 vil være af størrelsesordenen
10-5 og vil være af størrelsesordenen
10-5 og 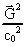 af
størrelsesorden 10-14. af
størrelsesorden 10-14.
Det kunne nu være interessant at beregne, hvor meget negativ masse
det gravitostatiske
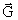 -felt omkring
jordkloden er ækvivalent med. Energitætheden Ug
(J/m³) er i afstanden r fra centrum af jorden givet ved: -felt omkring
jordkloden er ækvivalent med. Energitætheden Ug
(J/m³) er i afstanden r fra centrum af jorden givet ved:
(67) 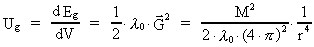
idet
(68) 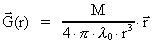
Ved integration fra jordoverfladen til uendelig fås for den totale
energi Eg i feltet:
(69) 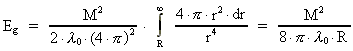
Her er R partikelradius (jordens radius) og M partikelmasse (jordens masse).
Da det stadig bemærkes, at
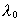 er
negativ, er den totale energi i feltet negativ. Udtrykt ved Newtons
gravitationskonstant G kan vi skrive: er
negativ, er den totale energi i feltet negativ. Udtrykt ved Newtons
gravitationskonstant G kan vi skrive:
(70) 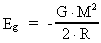
Dette udtryk svarer formelt til den potentielle energi af en partikel med
massen M, der befinder sig i afstanden 2R fra en anden partikel også
med massen M. Energien (70) er ækvivalent med en negativ gravitationel
masse
(71) 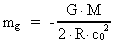
Ved benyttelse af værdierne M = 1024 kg; R = 6·106 m;
G = 6.6·10-11 Nm²/kg² fås en negativ masse
af størrelsesordenen mg = -1014 kg.
Positive og negative massers vekselvirkning
I dette afsnit vil vi undersøge, hvordan negative og positive masser
vekselvirker med hinanden. I første omgang vil vi antage, at
ækvivalensprincippet er gyldigt. Dette medfører, som tidligere
bemærket, at en negativ gravitationel masse må tillægges
en negativ inertiel masse. Lad os betragte en positiv gravitationel masse
mg, der befinder sig i feltet fra en fast positiv gravitationel
masse Mg.
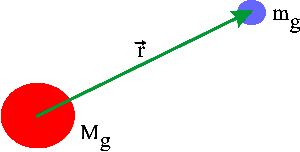
Bevægelsesligningen for mg er givet ved
(72) 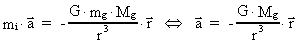
hvilket giver en acceleration 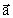 , som er rettet imod M. , som er rettet imod M.
Nu betragter vi en negativ gravitationel masse -mg; denne vil
have bevægelsesligningen
(73) 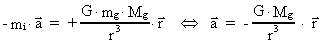
hvilket også giver en acceleration, der er rettet mod M.
Lad os nu betragte en negativ gravitationel masse -Mg, der er
fast (ved hjælp af understøtningskræfter f.eks.).
Lad i feltet af denne først en positiv, dernæst en negativ masse
bevæge sig. Den positive masse har bevægelsesligningen
(74) 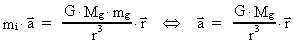
altså en acceleration
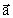 bort fra
massen M. Den negative masse har bevægelsesligningen bort fra
massen M. Den negative masse har bevægelsesligningen
(75) 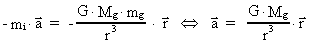
hvilket også bevirker en acceleration bort fra M.
Resultaterne (72) til (75) er baseret på, at ækvivalensprincippet
er generelt, således at vi må operere med negativ inertiel
masse. Hvis vi lader ækvivalensprincippet indskrænkes til kun
at gælde for positive gravitationelle masser, og således
tillægger en negativ gravitationel masse en positiv inertiel masse,
får vi følgende gravitationelle vekselvirkning: Gravitationelle
masser med samme fortegn tiltrækker hinanden, hvorimod masser med
modsat fortegn frastøder hinanden.
I forrige afsnit betragtede vi en hvilende graviterende masse. Hvis en
gravitationel masse bevæger sig i forhold til en iagttager, vil der
foruden et
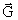 -felt også
være et -felt også
være et
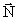 -felt. Den
energitæthed Ug,
der er i feltet, er da givet ved -felt. Den
energitæthed Ug,
der er i feltet, er da givet ved
(76) 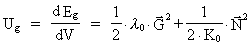
Da K0 også er negativ, vil energitætheden givet ved
(76) også være ækvivalent med en negativ masse.
Næste artikel
Hovedsiden
|